컴퓨터에게 0.1 이 0.1 이 아닌 이유

우리는 10진수의 세상에 산다

1을 10등분하면 0.1이라고 한다.

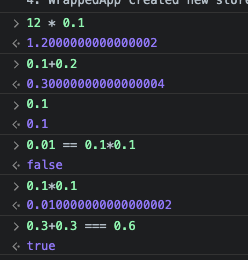
근데 자바스크립트는 0.1을 어려워한다. 0000000000000001 같은 숫자는 뭘까?

적어도 0.1이 우리가 아는 1을 10 등분한 0.1이 아님을 알 수 있다.

gpt에게 물어보자

"자바스크립트는 부동 소수점 숫자를 표현하기 위해 IEEE 754 표준을 따릅니다. 이 표준은 부동 소수점 숫자를 이진수로 표현하고, 특정한 비트 패턴을 사용하여 소수점 위치와 지수를 표현합니다. 하지만 이진법으로 정확하게 표현할 수 없는 일부 십진수 숫자들이 있습니다. 예를 들어, 0.1은 이진법으로 정확하게 표현할 수 없는 숫자입니다. 따라서, 자바스크립트에서 0.1을 정확하게 표현하는 데에는 제한이 있습니다."

무슨 소리인지 모르겠다. 일단 0.1을 2진수로 바꿔보자

https://woo-dev.tistory.com/93

블로그를 보니 소수점을 2진수로 계산하는 방법이 나와있다. 손으로 하면 힘드니까 이것을 함수로 만들어서 엄청나게 많이 반복해 보자

function floatToBinary(num) {
  let fractionalPart = Math.abs(num);
  let fractionalBinary = '';
  let precision = 1000;

  while (fractionalPart > 0 && precision > 0) {
    const product = fractionalPart * 2;

    if (product >= 1) {
      fractionalBinary += '1';
      fractionalPart = Math.floor((product - 1) * 10) / 10;
    } else {
      fractionalBinary += '0';
      fractionalPart = Math.floor(product * 10) / 10;
    }
    precision--;
  }

  return fractionalBinary;
}

나는 0.1~0.9만 테스트해 볼 생각으로 많은 로직을 생략했다.

소수점에 2를 곱하고 1을 넘어가면 1을 추가하고 2를 곱해도 0.~~~ 의 소수점이면 0을 추가하고 넘어간다

루프를 탈출하는 방법은 product가 1이 되어서 fractionalPart가 0이 되어 루프를 탈출하는 것뿐이다.

Math.floor((product - 1) * 10) / 10;

10을 곱하고 다시 10을 나누는 이유는 계산과정에서 부동소수점 2진수 표현문제로 오차가 발생해서 

정확한 결과를 얻을 수 없기 때문이다. 마지막까지 보면 이해가 된다.

 

위 함수를 반복하면 소수점을 2진수로 변환하는 것이 된다. 0.1을 2진수로 변환해 보자

10000번 반복해 보면 00011이 반복되는 무한소수가 나온다.

사실 손으로 해도 충분히 알만한 결과였다. 0.1 -> 0.2 -> 0.4 -> 0.8 -> 0.6 -> 0.2 -> 0.4 -> 0.8 ->.....  반복

결국 0.1을 2진수로 변환하면 끝을 낼 수 없는 무한소수가 나온다.

자바스크립트에서 숫자는 64비트의 메모리 용량을 가지므로 표현할 수 있는 한계가 있다. 

정확히는 64비트 중에 52비트만 가수를 표현하는 비트라고 한다.

컴퓨터의 한계가 아니라 수학적 한계 때문에 소수의 2진수는 근사치로 표현할 수밖에 없는 것이다.

 

그러면 위에서 10을 곱하고 10을 나누는 로직을 지우고 콘솔에 실제 계산과정을 찍어보자

function floatToBinary(num) {
  let fractionalPart = Math.abs(num);
  let fractionalBinary = '';
  let precision = 1000;

  while (fractionalPart > 0 && precision > 0) {
    const product = fractionalPart * 2;

    if (product >= 1) {
      fractionalBinary += '1';
      fractionalPart = product - 1;
      console.log(fractionalPart);
    } else {
      fractionalBinary += '0';
      fractionalPart = product;
      console.log(fractionalPart);
    }
    precision--;
  }

  return fractionalBinary;
}

0.1이 0001100110011001100110011001100110011001100110011001101 라는 결과가 나왔다.

콘솔을 보자

0.8에 2를 곱하는 순간 오차가 발생하기 시작한다

아주 적은 오차로 시작해서 곱하기 2씩 하면서 반복되다가 어느 순간 0.8이 0.8125가 되었다.

0.8125는 1.625이고 0.625 *2는 1.25가 되고 0.25*2는 0.5가 되고 0.5*2는 1이 되어 마무리된다.

계산과정에서 소수를 2진수로 표현하는 과정에서 오차가 생기고 이것이 쌓여서 잘못된 계산결과로 루프가 마무리된다.

이런 아주 작은 오차를 제거하고 실제 2진수로 바꾸는 계산과정을 재현하기 위해 

Math.floor((product - 1) * 10) / 10;

가 들어가 있다.

소수의 2진수는 무한하기 때문에 유한한 메모리로 표현할 수 없으므로 근사치로 표현된다.